Sam Lishak, sam.lishak@physicsx.ai
Albert Matveev, albert.matveev@physicsx.ai
Michalis Michaelides, michalis.michaelides@physicsx.ai
Abstract
Physical modelling allows precise and simple descriptions of nature, yet large- scale simulation of these models can be computationally expensive. For most of the last century, traditional numerical methods have dominated these efforts. However, with recent advancements in hardware, machine learning methods, and data collection strategies, new paths to modelling macroscopic physics have opened up. We review below some of the most promising new approaches and discuss our own preferences in this broader context. We believe that machine learning methods will fundamentally transform the landscape of physical simulation.
1.0 Introduction
Over the span of two millennia, humanity has developed a wide range of mathemat- ical models to understand, predict, and control natural phenomena. In this quest to model our world, interpretability and simplicity have been guiding principles. Large, intractable problems are decomposed into the sum of smaller, tractable parts. This has proved immensely powerful for modelling nature, and yielded tremendous advancement in fundamental understanding: microscopic building blocks that, when put together, can reconstruct the stunning macroscopic complexity that emerges.
Despite the (almost absurd) effectiveness of this approach, it still suffers from the curse of composition: putting all those little parts together to construct the whole picture is a painstaking endeavour, which requires great care and computational effort. We have access to fundamental rules, but we still need to play them out to recover the outcome. This is known as simulation and is a commonly employed technique in physical mod- elling: known PDEs provide local rules and solvers recover the global outcome.
1.1 Traditional methods for physics
Simulation methods are employed to resolve the behaviour of matter (solids, fluids, gases, etc.), fields (electromagnetic, pressure, velocity, density), and any number of other physical phenomena that are driven by known local rules, particularly partial differential equations (PDEs). Therefore, traditional simulation methods typically involve some kind of discretisation of the physical domain of interest, such that the rules of the governing PDE can be locally well-approximated by a tractable computation. Local computations are stacked together and iterated upon until we converge to a solution. Beyond a narrow class of problems where a closed-form solution can be provided, this is generally how complicated problems are addressed. Many PDEs can exhibit chaotic behaviour in their full form, which often causes us to resort to simpler approximations at the PDE level, even before discretisation, to make them computationally feasible and ensure convergence.
Constructing global solutions from known local relationships is an adaptable strategy as it can be applied to a wide range of problems. However, it suffers from great com- putational cost and the need to resolve each setting or boundary condition via further iteration, besides palliatives like seeding the solver with a previously computed solution of a similar problem as an initial condition.
This leaves a lot of room for improvement, especially given the iterative workflow in typ- ical engineering. Consider, for example, an engineering task like the design of a wing to maximise aerodynamic efficiency under some constraints. It involves searching through a space of possible designs, where for each design the PDE needs to be expensively re- solved to recover the quantities of interest. Furthermore, that design space can be very large, while solutions can be relatively similar between designs. These characteristics suggest that there might be a better way to approach this problem.
1.2 Machine learning methods for physics
The field of machine learning (ML) has grown tremendously over the past half cen- tury and has profoundly impacted scientific endeavour. It has enabled investigations that were previously inconceivable and has been applied on a range of domains with surprising success. Much of that success has to do with the abundance of data that cover the domain of application. As such, computational advancements (and to some extent methodological advancements) allow us to exploit the available data to better fit relationships and capture phenomenological patterns, in a way that was historically impossible.
An axis on which ML methods can be placed ranges from supervised to unsupervised methods. On the supervised end, there are methods that seek to learn a mapping from one domain to a co-domain, when presented with many paired instances; on the unsupervised end, there are methods that seek to capture the generative distribution of the observations, often with only weak assumptions about its structure. Methods of both kinds find applications in many domains: the recent advancements in language and image generation belong mostly in the latter category, but also borrow concepts from supervised learning. There are advantages and disadvantages across the spectrum, but one notable difference is that some unsupervised methods allow you to generate new synthetic observations, without requiring an input, or only given a partial input. However, they tend to be harder to fit to data and often require more data to recover something well-behaved.
Reflecting on the typical engineering workflow, it is apparent how such methods might be of use. One can train ML models to produce solutions given the problem setting, or even learn the entire joint distribution of settings and solutions such that the model can simultaneously produce both a novel setting and its solution. In our example of designing a wing, supervised learning would involve learning the mapping of wing designs to the field solutions, or derived quantities of interest. Unsupervised learning would instead aim to capture the joint distribution of both wing designs and solutions in the dataset, and as such be able to generate novel designs and their associated solutions at once. Alternatively, we can split up the problem into an unsupervised part for learning the distribution of problem settings, and a separate supervised part to associate settings to solutions.
We outline some of these options below. Particular choices aside, ML methods in gen- eral provide a new approach to accomplishing engineering tasks. Any of these methods greatly accelerate iterations in the design optimisation workflow, as they allow us to search the space faster and guide our search towards promising areas. This results in bet- ter exploration, overall lower computational costs for simulating physics, and ultimately, higher quality designs in a shorter time-frame and with lower manual effort.
2.0 A list of our favourite things
We start with the simplest setup of mapping problem settings to solutions of PDEs, or quantities of interest (QoIs) derived from those solutions. The most general framing for this supervised learning task is to learn a function that maps from boundary conditions and PDE parameters to the solution of the PDE or to derived QoIs. While we have a large number of methods to choose from, almost all of them impose some conditions on the input and output of this mapping. Most ML methods expect fixed-length vectors for both input and output, which introduces some challenges for the kind of input we want. Consider how we might want to map boundary conditions that depend on complex geometric shapes to fields over a continuous domain, where representations of both the input and the output are not vectors. Figure 1 illustrates a set of learning tasks that present this challenge.
2.1 Geometric and operator deep learning
One approach to solving PDEs on and around geometry is to adopt models that can take as input structures that are better suited at representing geometries and other PDE settings, such as point clouds, graphs, meshes, or fields (see Figure 2). An extensive body of literature exists to define architectures for such inputs (Bronstein et al., 2017, 2021), where a lot of effort was put into introducing efficient, yet expressive, ways to extract information from arbitrarily sampled data. For a given geometry, they allow us to directly map a representation, be it mesh, signed distance function, or occupancy field, to a QoI, or even to an entire field output. Most notably, Graph Neural Networks (GNNs) (Scarselli et al., 2009) revolutionised how researchers think about model design and gave rise to a vast family of models (Masci et al., 2018; Pfaff et al., 2021; Sharp et al., 2022). Despite the ever-changing research landscape, they stood the test of time. Even the more recent and more complicated models aim to exhibit the same desirable properties as GNNs: they are not sensitive to input size or order, and allow information to spread efficiently.
It is also unsurprising that with slight tweaking GNNs can become much more suitable for creating physics surrogates. A fairly fresh research direction is the development of Neural Operators (NOs) (Li et al., 2020, 2021; Cao et al., 2023; Kovachki et al., 2023). These models are concerned with approximating more general mappings than standard neural networks and exhibit several theoretically appealing properties. NOs map fields to fields, rather than vectors to vectors, despite training on discretised data, in such
Learning tasks on various geometric domains. Left: mapping an input field to an output field on a flat domain (Darcy flow problem of mapping a given permeability field, top, to its flow pressure solution, bottom); middle: mapping an input field to an output field on the closed surface of a geometry (input coordinate field of artificial heart pump, top, to pressure, bottom); right: same as middle, but mapping to the pressure signal over the entire domain (pressure in volume, bottom).
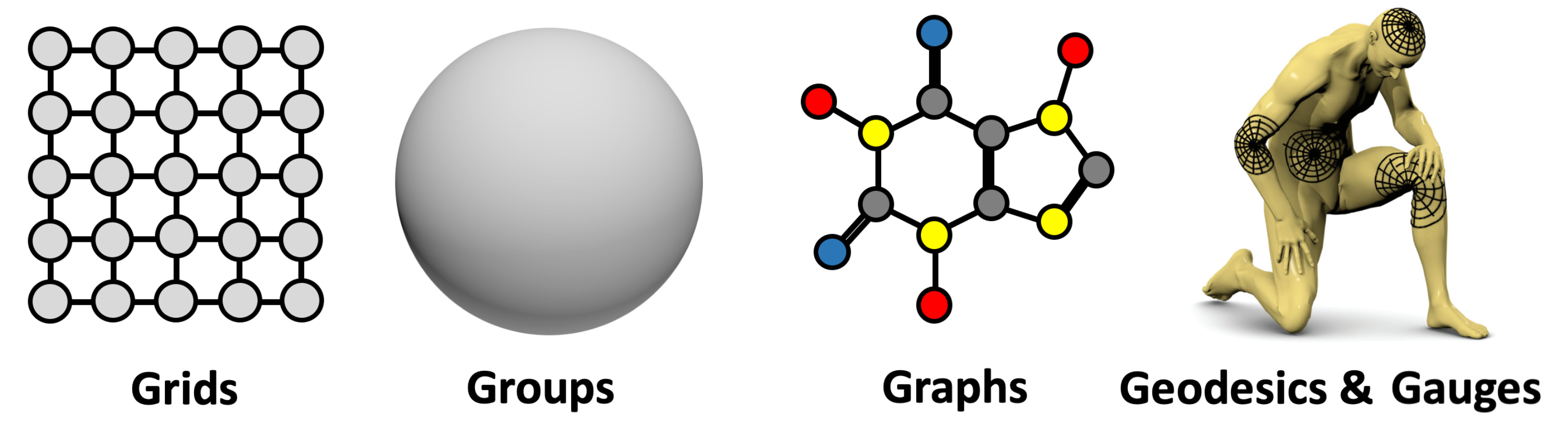
The 5G of Geometric Deep Learning: grids, groups & homogeneous spaces with global symmetry, graphs, geodesics & metrics on manifolds, and gauges (frames for tangent or feature spaces). Presented as Figure 9 in (Bronstein et al., 2021). a way that they can recover mappings with arbitrary precision independently of input resolution. This exceptional expressive power makes them a perfect building block for modelling PDE solutions. Even though the first NO was based on a GNN architecture, the line of thought went further, and more advanced mathematical concepts are now employed to extend the flexibility of these models. Figure 3 illustrates the main idea behind most NO architectures.
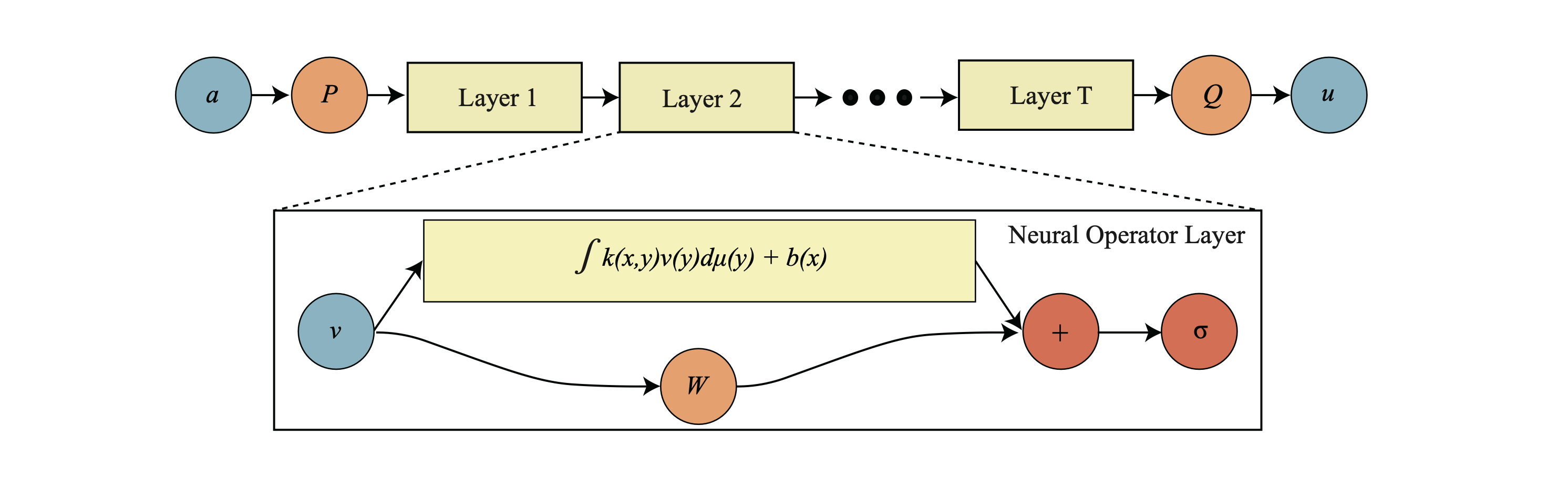
Neural operator architecture schematic. The input function a is passed to a point-wise lifting operator P that is followed by T layers of integral operators and point-wise non-linearity operations σ. In the end, the point-wise projection operator Q outputs the function u. The choice of method to perform the convolution operation yields various flavours of this neural operator architecture. Note that the kernel is parametrised by a NN. Presented as Figure 2 in (Kovachki et al., 2023).
Methods of this kind have become favourites in our toolkit over the past few years, especially certain flavours of GNNs and NOs. However, these models are still quite niche and immature compared to the larger set of ML methods available for vectorised representations. As such, we do a lot of work to overcome challenges in scaling to the mesh size commonly found in engineering (∼1M-100M vertices) and effectively use geometric priors such that we can learn efficiently from limited data sizes.
2.2 Generative Models
In a different vein, we can try to recover a vectorised representation of the geometric boundaries and parameter inputs that allows us to use standard ML methods, where a lot of work has already been done to overcome challenges like scaling, or learning efficiently from limited data. However, we here face the problem of translating data like geometric meshes and fields into vectors.
One idea is to use the computer-aided design (CAD) parameters that generate the geometries in the first place, but there are associated difficulties: for instance, CAD parametrisation can be different between geometries even within a particular task. Fur- thermore, CAD parametrisations are only useful for describing constructed geometries, not input fields like initial conditions, or empirical data like scanned geometries.
Unsupervised learning methods can be powerful techniques for translating these dis- parate data formats into vectors in a common low-dimensional space, such that the vectorised representations capture the variation observed in the data. We find that this embedding recovers a particularly useful representation for downstream engineering tasks, like associating those embeddings with QoIs.
If we further model the distribution of these embeddings, we can even generate novel geometries drawn from the same distribution as the observations — this is essentially a generative model for a particular set of geometries that is of interest. This low- dimensional space of geometries is also often easier to search through than a CAD or mesh representation, and can therefore serve as the design space over which we optimise.
This requires a map to go from a (latent) vector representation to a geometry, which is often learnt simultaneously with the latent embeddings. A promising approach is to learn a neural implicit geometry representation, for example a Signed Distance Function (SDF) as in Park et al. (2019). The work of Seidman et al. (2023) paves the way for Variational Auto-Encoders (VAEs) to meet this task, while retaining the flexibility of working with the SDF functional representation for geometries (see Figure 4 for samples drawn from a VAE trained on a particular function class).
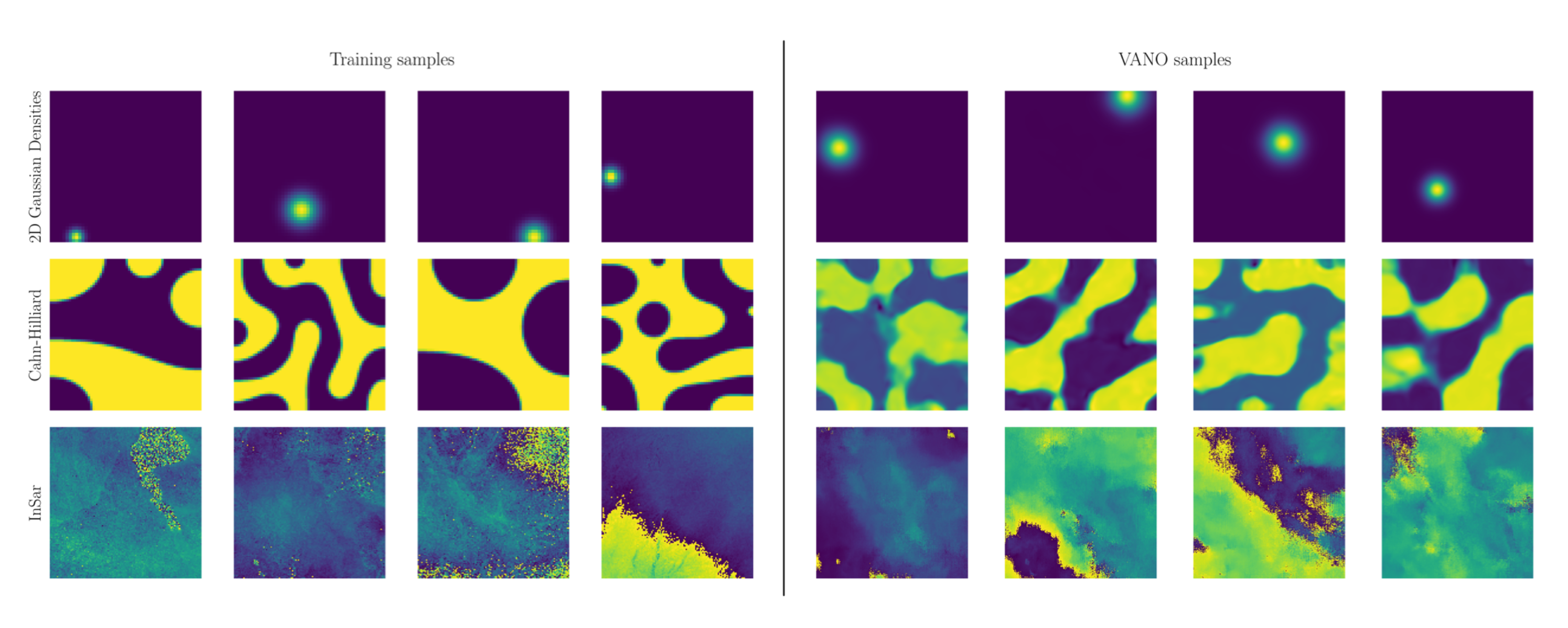
Representative function samples from the different benchmarks considered in this work. Left: Example functions from the testing data-sets, Right: Super-resolution samples generated by VANO. Presented as Figure 2 in (Seidman et al., 2023).
VAEs and other generative models require careful experimentation to apply in our prob- lem settings, but we found that with appropriate tuning they are capable of representing the data we work with (e.g., geometries and fields) at the required fidelity for down- stream engineering tasks.
2.3 Physics-informed models
The models discussed so far do not leverage the fact that we often know the PDE that generates data and governs solutions; the focus has been to approximate the physical laws from observations, rather than impose them in the model structure explicitly. This is primarily because of the difficulty of incorporating such prior knowledge into the models, but also because simulation data may disobey the exact PDE due to the ap- proximations required to facilitate numerical simulations. However, a new approach to simulation has recently been proposed that takes advantage of this prior knowledge in an effort to reduce data requirements and promote physically consistent solutions. Physics- Informed Neural Networks (PINNs), as presented by Raissi et al. (2017b,a); Zhu et al. (2019); Karniadakis et al. (2021) introduces an artificial neural network (ANN) that takes as input the coordinates of any point in the domain of the PDE, and outputs the value for the solution field at that point. The ANN is tasked with representing the solution field, and is trained by sampling points randomly in the domain and penalising deviations from the PDE at those points. As long as the activation function of the ANN is sufficiently differentiable, residuals in the terms of the PDE can be easily evaluated, which can be combined into the loss function to be minimised with respect to the ANN parameters. The ANN is an ansatz about a parametrised form of the solution (albeit a particularly flexible one) and we attempt to fit the parameters such that it best matches the PDE. The idea harks back to older variational numerical simulation methods, like the generalised Galerkin approximation and others.
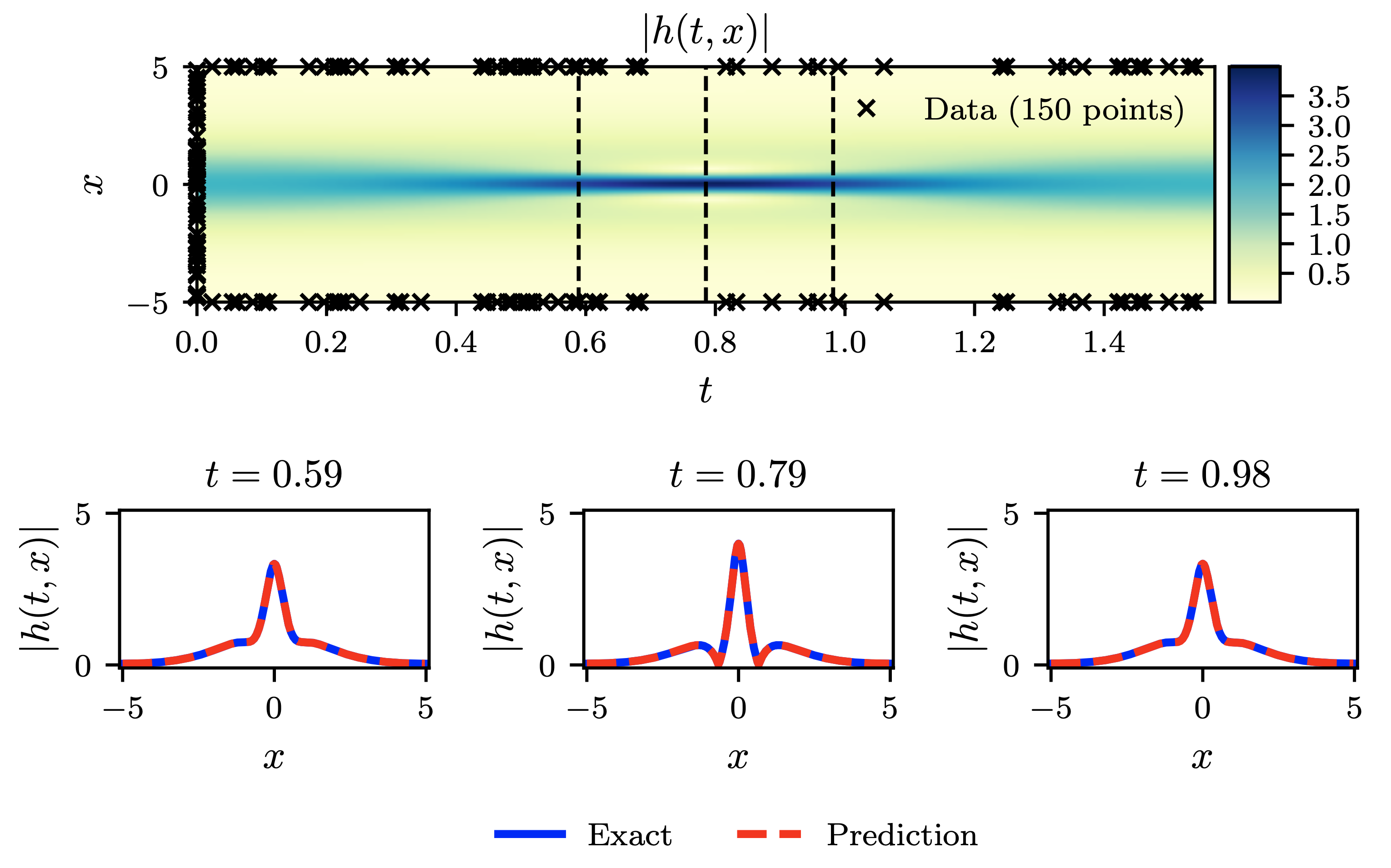
Shrödinger equation: Top: Predicted solution |h(t, x)| along with the initial and boundary training data. In addition, 20,000 collocation points generated using a Latin Hypercube Sampling strategy for the PINN loss. Bottom: Comparison of the predicted and exact solutions corresponding to the three temporal snapshots depicted by the dashed vertical lines in the top panel. The relative L2 error for this case is 1.97 · 10−3. Presented as Figure 2 in (Raissi et al., 2017b).
In the same spirit, the ANN can be made to represent an SDF rather than a PDE solution, where ANN parameters can be tuned to recover a useful geometry in what are termed Geometry-Informed Neural Networks (Berzins et al., 2024). For example, one can optimise the SDF-ANN for given geometric objectives and constraints using a gradient-based method to obtain the design of a bracket that remains attached to anchor points while minimising internal volume.
It should be emphasised that, while there are hybridisations that blend data-driven learning with physics-informed solutions, PINNs in their pure form essentially substitute discretised domain solvers for PDEs with a different kind of solver that uses ML techniques to converge to a solution; for every new setting presented, this method still needs to iterate until convergence. In testing, we found that a pure PINN approach struggles with complicated geometries and boundary conditions and is sensitive to the choice of sampling scheme for collocation points where PDE errors are computed. How- ever, this approach can be powerful in conjunction with data-driven approaches to induce physical biases in the model — for example, by incorporating the PDE residual loss in an otherwise data-driven model — especially when a prediction of behaviour is sought well beyond the coverage afforded by the training dataset.
3 Conclusions
We have outlined a selection of methods in ML that can prove beneficial in the domain of physics and engineering. This framing of physics problems and the suggestions for tackling it are not new, but instead reflects a current of proposals throughout the past couple of decades by many academics. In our review of the more prominent and promis- ing approaches we paid special attention to the ones that have proven most useful to us, like GNNs for supervised learning on meshes, and VAEs for unsupervised embedding of geometric boundary conditions.
These approaches have not yet been widely adopted outside of academia, possibly be- cause of previous limitations in compute and method maturity for these to supplant traditional engineering workflows in design and engineering. We are committed to bringing about this change, as we believe that it will yield significant benefits and expand our ability to search design spaces across the whole domain of engineering, from design and manufacturing, to testing and diagnostics. We also believe that these approaches will unlock design paradigms, like automated workflows and privacy-preserving data pooling, as well as make possible novel applications that were before infeasible through better exploration of the solution space.